The spelled-out intro to neural networks and backpropagation: building micrograd

Micrograd là một autograd engine (công cụ tính đạo hàm tự động) đơn giản, triển khai thuật toán backpropagation - thuật toán cốt lõi giúp cải thiện độ chính xác của các mô hình máy học. Hiện nay, backpropagation là nền tảng toán học quan trọng nhất của bất kỳ thư viện deep learning hiện đại nào.Trong series này, chúng ta sẽ cùng tìm hiểu về neural networks từ những cơ sở toán học cho đến việc cài đặt các hàm số cơ bản và xây dựng thuật toán backpropagation. Thông qua series này, bạn sẽ hiểu sâu về nền tảng của AI nói chung và deep learning nói riêng, đồng thời có thể tự xây dựng một thư viện để phát triển các mô hình machine learning, deep learning, và thậm chí là một mô hình tương tự ChatGPT.

Derivative - Đạo hàm

Đạo hàm bậc một

thấy ghê...

Nói đơn giản, ta lấy một giá trị $h$ rất nhỏ, tính sự thay đổi $f(x+h) - f(x)$, rồi chia cho $h$ để biết tốc độ thay đổi (hay độ dốc) của hàm số tại điểm $x$. Từ đó ta biết được hàm số đang tăng hay giảm và tăng/giảm nhanh như thế nào.

Khi giá trị $\frac{f(x+h) - f(x)}{h}$ âm, giá trị của hàm $f(x)$ có xu hướng giảm dần. Ngược lại, giá trị $\frac{f(x+h) - f(x)}{h}$ lớn hơn 0, giá trị của hàm $f(x)$ có xu hướng tăng dần. Và nếu bằng 0 thì hàm số không đổi bất kể $x$ là bao nhiêu.

Lấy ví dụ, với hàm số $f(x) = 3x^2 - 4x + 5$, ta lấy $x_1=3$, $x_2=-3$, $h=0.2$, thay vào hàm $f(x)$ và nhận xét.

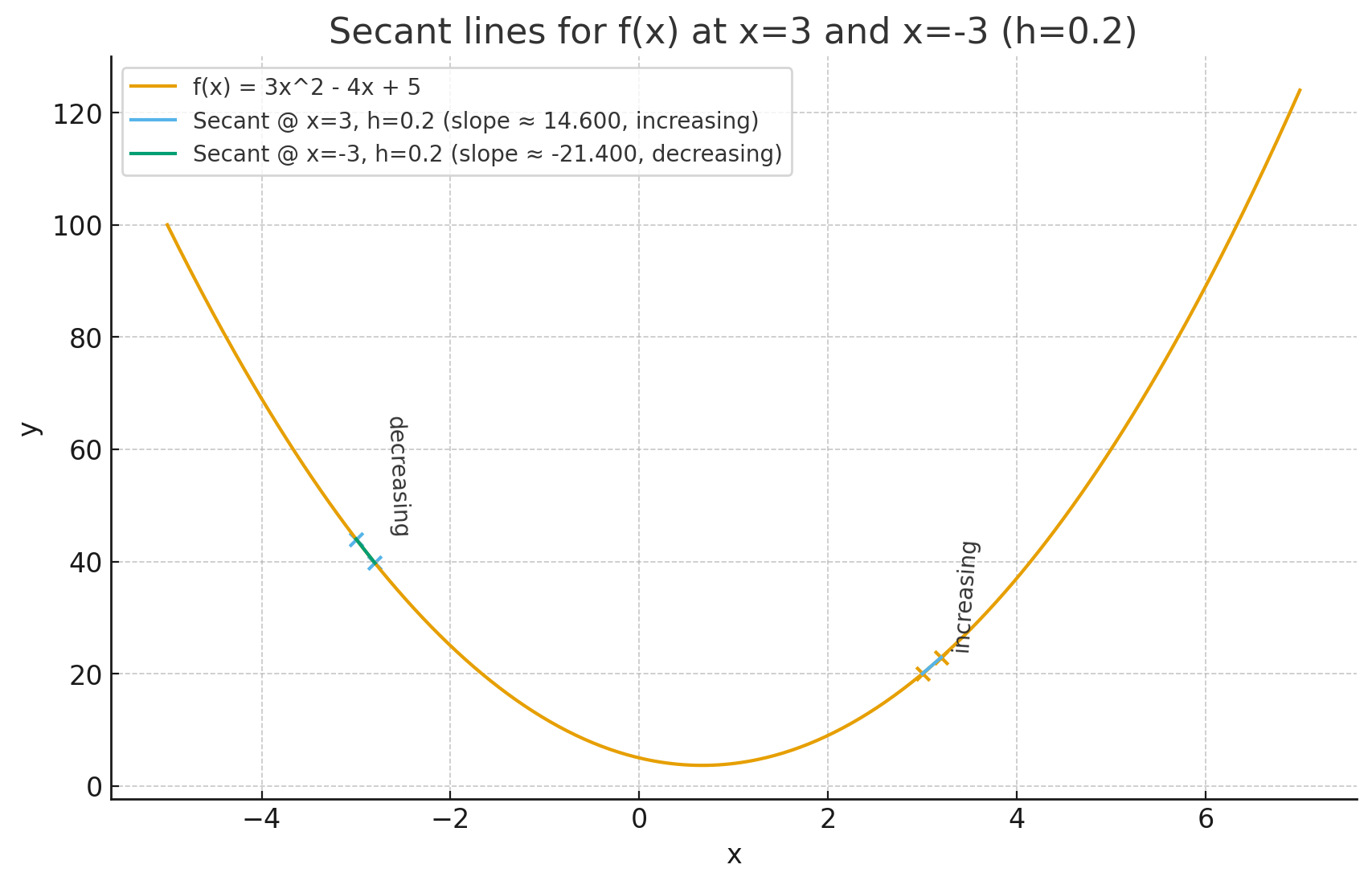
Hình 1: Ví dụ sự tăng giảm hàm số

Với cặp điểm $[x_1, f(x_1)]$ và $[x_1+h, f(x_1+h)]$ thì hàm số có xu hướng tăng lên, cũng như với công thức:

$L = \frac{f(x_1+h) - f(x_1)}{h} = \frac{22.92 - 20}{0.2} \approx 14.6 > 0$

Trong thực tế, ta lấy $h$ rất rất nhỏ và hàm số $f$ rất phức tạp và không chỉ có mỗi $x$.

Đạo hàm riêng

Với những hàm số có nhiều biến, mình hiện tại có thể xem độ đốc của từng biến. Lấy ví dụ:

a = 2
b = -10
c = 5
h = 0.0001

d1 = a*b + c
d2 = (a+h)*b + c

Thì hàm số d2 có xu hướng tăng hay giảm?

Tuy nhiên giải pháp này nhìn thì có thể chưa tổng quát lắm, thực tế số lượng biến trong một hàm số thể lên tới hàng tỷ và việc lấy giấy bút ra tính đạo hàm, thay số, tính giới hạn,... có vẻ không tối ưu lắm.

Khởi đầu của micrograd và hình thù của nó

Để biểu diễn các phép toán phục vụ backpropagation, ta cần có một cấu trúc dữ liệu thích hợp, và ở đây ta sử dụng cấu trúc dữ liệu cây để thể hiện được rõ sự liên kết giữa các node.

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self._prev = set(_children)
        self._op = _op
        self.grad = 0
        self.label = label

    def __repr__(self):
        return f"Value(data={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data, (self, other), '+')

    def __mul__(self, other):
        return Value(self.data * other.data, (self, other), '*')

Giả sử ta có phép toán sau:

$a = 20, b = -3.0, c = 10.0 \\ e = a * b \\ d = e + c \\ f = -2.0 \\ L = d * f$

Biểu diễn dưới dạng code

a = Value(2.0, label='a')
b = Value(-3.0, label='b')
c = Value(10.0, label='c')
e = a * b; e.label = 'e'
d = e + c; d.label = 'd'
f = Value(-2.0, label='f')
L = d * f; L.label = 'L'

Và đây là hình thù của nó khi ta vẽ ra

Hình 2: Biểu diễn toán học

Thông thường, $L$ đại diện cho hàm loss, mục tiêu của chúng ta là làm cho nó "mất càng ít càng tốt". Để làm được điều đó, đầu tiên ta cần phải tính "độ nhạy của L" với từng biến số như thế nào thông qua gradiant.

Nhìn hình 2, đầu tiên ta có thể tính "độ nhạy của $L$ với $d$" hay nói đúng hơn là đạo hàm của $L$ với $d$ bằng công thức đã học ở THPT và Vi tích phân ở đại học:

$\frac{dL}{dd} = d * f \frac{d}{dd} = f$

Ta có thể chứng minh được bằng công thức thực tế ở đầu bài:

$\frac{L_2 - L_1}{h} = \frac{((d + h) * f) - d * f}{h} = \frac{((4.0 + 0.0001) * (-2.0)) - 4.0 * (-2.0)}{0.0001} \approx -2$

Tương tự với

$\frac{dL}{df} = d f \frac{d}{df} = d$

Thêm vào công thức ban đầu, ta có được:

Hình 3: Biểu diễn toán học với Gradiant

Tiếp tục với các biến khác, ta cần tính $\frac{dL}{de}$.

Áp dụng chain rule

$\frac{dL}{de} = \frac{dL}{dd} \cdot \frac{dd}{de}$

$\frac{dL}{dd}$ thì mình có rồi, còn $\frac{dd}{de}$ mình dễ dàng tính được bằng cách dùng công thức đã học. Kết quả tìm được là:

$\frac{dL}{de} = f \cdot 1 = f$

Tương tự cho tới hết những giá trị, mình được một cây với đầy đủ các giá trị gradiant

Hình 4: Biểu diễn toán học với đầy đủ giá trị Gradiant

Thực tế thì mấy ai lại đi chạy bằng tay như thế, nên ta cùng tự động hoá quá trình này nhé! Thông qua quá trình tính toán ta thấy một framework chung là tính dữ liệu chiều đi trước, sau đó quay ngược lại để tính gradiant dùng đạo hàm cục bộ (local gradiant) và nối kết quả với từng tham số qua chain rules.

Phép cộng

Ví dụ, mình có một biểu thức đơn giản $c = a + b$. Vì đạo hàm của $c$ theo $a$ hay đạo hàm của $c$ theo $b$ đều có kết quả là một hằng số, nên giá trị grad trong trường hợp này phụ thuộc vào grad của $c$.

# forward
a = Value(5.0)
b = value(2.0)
c = a + b

# backward
c.grad = 0.23
c._backward()

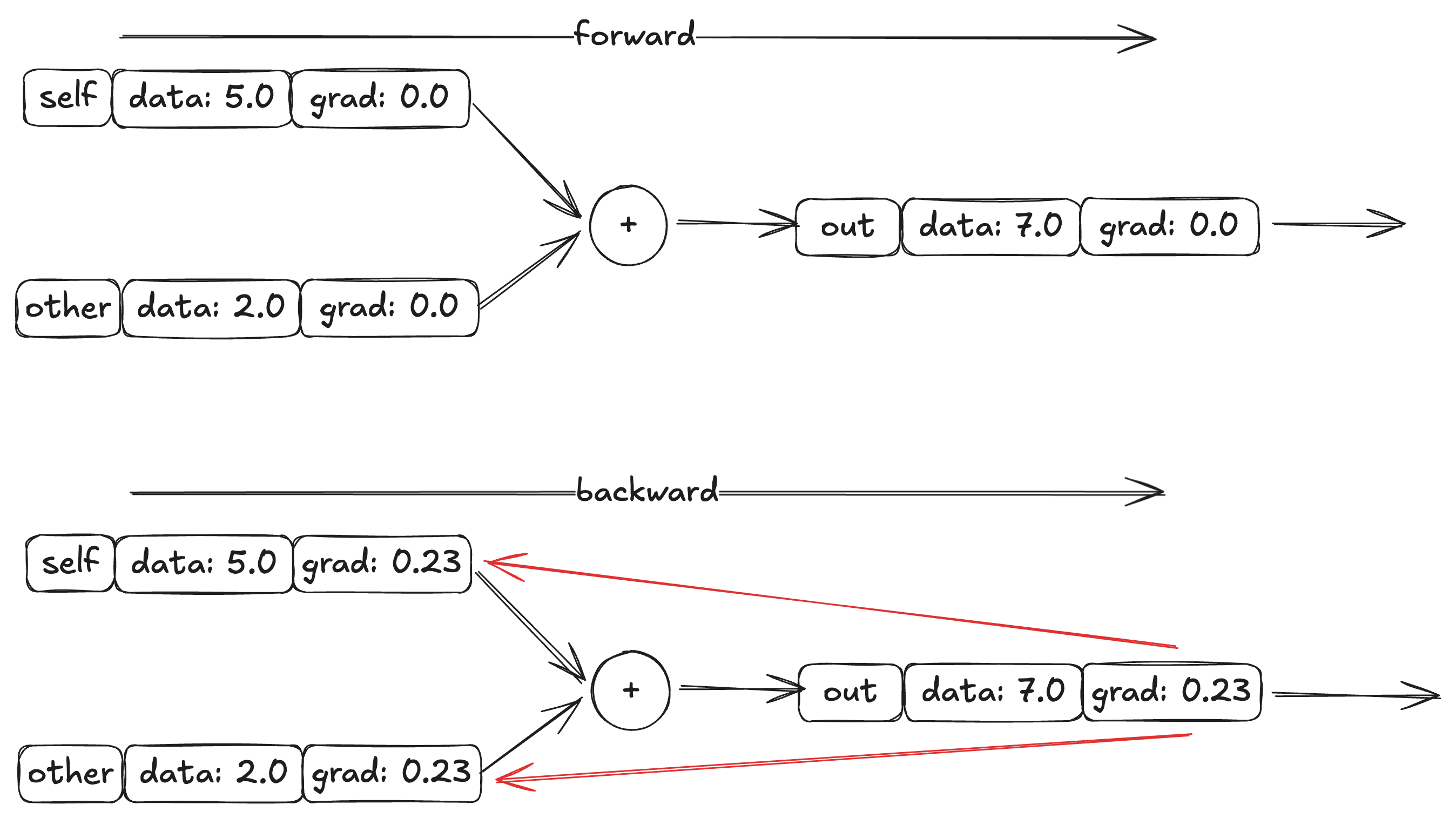
Hình 5: Backward $c = a + b$

class Value:
    def __init__(self, data, _children()):
        self.data = data
        self._prev = set(_children)
        self.grad = 0.0
        self._backward = lambda: None (1)

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other), '+')

        def _backward(): (2)
            self.grad += 1.0 * out.grad
            other.grad += 1.0 * out.grad

        out._backward = _backward
        return out

(1) Định nghĩa function mới là _backward để thực hiện đạo hàm, tính gradiant.

(2) Cài đặt đạo hàm cục bộ và áp dụng quy tắc chuỗi.

Phép nhân

Với phép nhân, ta quay lại một xíu bài tập ở phía trên.

$c = a * b$

$\frac{dc}{da} = b$

$\frac{dc}{db} = a$

Từ những đạo hàm riêng ở trên, ta thấy đạo hàm của từng giá trị riêng phụ thuộc vào data của giá trị còn lại. Nếu lấy $a=5.0$, $b=2.0$ thì

$\frac{dc}{db}|_{a=5.0} = 5.0$

$\frac{dc}{da}|_{b=2.0} = 2.0$

# forward
a = Value(5.0)
b = value(2.0)
c = a * b

# backward
c.grad = 0.23
c._backward()

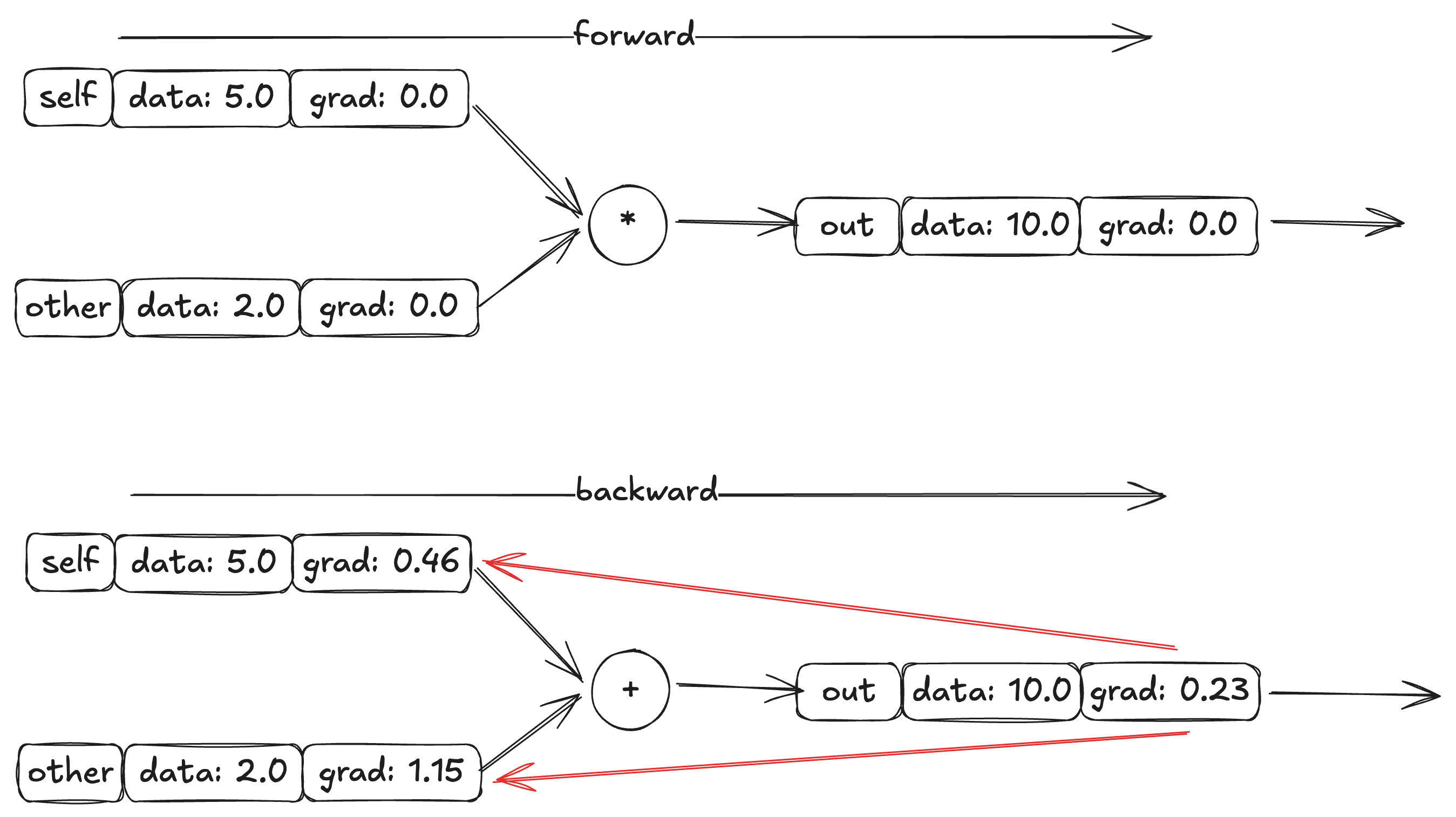
Hình 6: Backward $c = a * b$

Từ những dữ kiện trên mình xây dựng được hàm _backward() cho phép nhân.

Đừng quên chain rule nhé

class Value:
    def __init__(self, data, _children()):
        self.data = data
        self._prev = set(_children)
        self.grad = 0.0
        self._backward = lambda: None (1)

    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*')

        def _backward(): (2)
            self.grad += other.data * out.grad
            other.grad += self.data * out.grad

        out._backward = _backward
        return out

(1) Định nghĩa function mới là _backward để thực hiện đạo hàm, tính gradiant.

(2) Cài đặt đạo hàm cục bộ và áp dụng quy tắc chuỗi.

Đến đây ta đã làm được cho hai phép toán cơ bản nhất là cộng và nhân. Với một vài phép toán khác (ví dụ như trừ và chia) cũng chỉ là một dạng đặc biệt của phép cộng và nhân nên mình sẽ không cài đặt ở đây. Còn một vài phép toán hữu dụng mà bạn đọc có thể thử tự mình cài đặt như bài tập về nhà như phép log - logarit, exp - exponential ($e^x$), pow - luỹ thừa, các hàm lượng giác,...

Quay lại phép toán đầu bài, áp dụng _backward() để tính grad cho từng node.

# forward
a = Value(2.0)
b = Value(-3.0)
c = Value(10.0)
f = Value(-2.0)

e = a * b
d = e + c
L = d * f

# backward
L.grad = 1.0 # base case, hoặc mình có thể tự tính bằng công thức giới hạn L.grad = [L(x + h) - L(x)] / h
L._backward()
d._backward()
f._backward()
e._backward()
c._backward()
b._backward()
a._backward()

Hình 7: Backward manual

Tuy nhiên, việc gọi function từng node như thế này khá là bất tiện và việc xem node nào chạy trước cũng là một vấn đề. Để giải quyết vấn đề này, mình sẽ duyệt qua từng node theo thứ tự topologic xem ví dụ để đảm bảo việc thực thi sẽ đúng thứ tự, từ đầu tới cuối.

Xem thêm: https://www.interviewcake.com/concept/java/topological-sort

Cuối cùng, ta được một engine hoàn chỉnh, làm nền tảng cho neuron networks.

class Value:
    ...

    def backward(self):
        topo = []
        visited = set()

        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)

        build_topo(self)

        self.grad = 1
        for v in reversed(topo):
            v._backward()

Cuối cùng, thay vì có một chuỗi lời gọi hàm thì mình chỉ cần gọi L.backward() là gradiant sẽ tự động được lan truyền xuống các node con trong thuật toán backpropagation.